Banach *-algebra

In mathematics, Banach *-algebra A is a Banach algebra over the field of complex numbers, together with a map * : A → A called *-involution which has the following properties:

1. (x + y)* = x* + y* for all x, y in A.
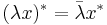2. for every λ in C and every x in A; here, 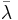denotes the complex conjugate of λ.
3. (xy)* = y* x* for all x, y in A.
4. (x*)* = x for all x in A.

Some authors include the following isometry condition in the definition:

• ||x*|| = ||x||.